

Figure Set 2: What are the effects of herbivory on population growth rate?
STUDENT INSTRUCTIONS
Population modeling is valuable tool to rapidly assess how ecological factors impact the population growth rate of a species. In this experiment population modeling is used to assess the potential effectiveness of biocontrol on the population growth rate of the invasive Lespedeza cuneata. Life cycle figures represent what size classes are represented in the study species and the possible transitions between these size classes. In this experiment there are four size classes and two types of seed that can contribute to a seed bank. The life cycle figures also highlight the potential transitions from one year to the next. For example, an arrow going from small to medium would indicate the transition from plants that were small in one year growing to medium plants in the following year. Data gathered from actual seed set and growth is used to calculate the probability of these transitions. These values can then be placed into a transition matrix; matrices are created for each treatment (see example below).
Population modeling is valuable tool to rapidly assess how ecological factors impact the population growth rate of a species. In this experiment population modeling is used to assess the potential effectiveness of biocontrol on the population growth rate of the invasive Lespedeza cuneata. Life cycle figures represent what size classes are represented in the study species and the possible transitions between these size classes. In this experiment there are four size classes and two types of seed that can contribute to a seed bank. The life cycle figures also highlight the potential transitions from one year to the next. For example, an arrow going from small to medium would indicate the transition from plants that were small in one year growing to medium plants in the following year. Data gathered from actual seed set and growth is used to calculate the probability of these transitions. These values can then be placed into a transition matrix; matrices are created for each treatment (see example below). Researchers can then incorporate matrix values into modeling programs, such as R (which is freely available on the internet) to calculate a value, λ, which represents the growth rate of a population under the conditions when the data was collected. λ is extracted fairly easily from the demographic matrix (it is the dominant eigenvalue of the matrix). A λ value which is below 1 represents a population that is declining, a λ value at 1 is a population that is at stasis (neither growing nor declining), and a λ value which is above 1 represents a population that is growing. One would predict that an invasive species, which is successful, would display a population growth rate (λ) which is above 1. Therefore a successful use of biological control would bring the population growth rate (λ) below 1.
Finally, elasticity analyses are used to determine what vital rates λ is most sensitive to. Elasticity matrices yield elasticity values for each vital rate. The highest elasticity value in the elasticity matrix is associated with the vital rate that λ is most sensitive to. Therefore, even small changes in this vital rate will result in significant changes to λ. Biological control is expected to be most successful at reducing the population growth rate (λ) when the vital rates that are affected by the control agent have high elasticity values.
1. Look over the example given below to understand how values from a life cycle graph go into a matrix.
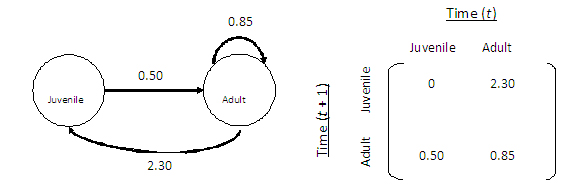
2. Spend a few minutes examining Figure 2 to ensure that you understand what the circles, arrows, and numbers represent. Then place the numbers where they belong in the control matrix (you can download and print Handout 1). Pair up with your neighbor to check your interpretation.
3. Follow the instructions below (also available as Handout 2) to use the R Program 'Lespedeza' to calculate the population growth rate (λ) of plants in the control treatment. Pair up with your neighbor to check that your lambda values are the same.
- If you haven't already done so, download R onto your computer from the website: http://cran.r-project.org/
- Make sure the file 'lespedeza' is also on your computer.
- Open R. You will see the R console.
- Open the file 'lespedeza' by clicking on file and then open script (for PC users) or by clicking on file and then open document (for mac users). Find the lespedeza file on your computer.
- Make sure you are in the lespedeza file (the R editor, not the R console).
For PC users: To run the program, click on edit and then run all. For mac users: To run the program, click on edit and then select all. Then click on edit and execute - Make sure you are in the console (IMPORTANT: DO NOT TYPE IN CODE, i.e. do not type in the Lespedeza file). Type in 'A' and hit return (note: this is case-sensitive), and you will see your matrix. Make sure this matrix is the same one you came up with in handout 1.
- Type in 'lambda' and hit return, and you will see the population growth rate associated with your matrix.
4. Fill in the bar graph below (you can download and print Handout 3) based on the results you calculated for the control treatment in R. Fill in the bar you make. Now make predictions based on possible hypotheses about how λ will change with the different treatments. Remember: a population growth rate (λ) below 1 is declining and above 1 is increasing.
5. Provide brief answers to the following questions or follow directions if indicated.
- Recall, which stage (or size of plants) was the only stage that was found to be significantly affected by the herbivory treatments?
- What was the direction of this effect? Explain.
- Given the population growth rate you found for the control treatment, the answers to questions a and b, and your expectations of biocontrol, what do you predict will happen to the population growth rate (λ) if you replace the transitions of small to medium plants in the matrix that were found for each treatment? Explain.
- Illustrate your answer to question b on the graph above. Do not fill in the bars.
6. When you are finished, compare your responses with your neighbor.
7. Follow the instructions below for changing data in the R Program to change the matrix, and re-calculate the population growth rate (λ) for each herbivory treatment. These instructions are also available as Handout 4.
- In your R program 'lespedeza', change the value in the matrix that corresponds to the small to medium transition (i.e., this one should have an initial value of 0.64). Once you have made the change, re-run the program (For PC users, edit and run all; For mac users, edit and select all, then edit and execute). Switch back to your console, and type in 'A' to see your revised matrix. Check the revised matrix to observe your change was made properly. Next, type in 'lambda' to see the population growth rate associated with that matrix.
Treatment |
Small-Medium Transition Probability |
Control (0%) |
0.64 |
20% |
0.62 |
40% |
0.31 |
60% |
0.39 |
80% |
0.23 |
8. Compare your findings with your neighbor and then individually complete the questions and figure below regarding the population growth rates of the invasive Lespedeza cuneata in different clipping treatments. The questions and figure are available as Handout 5.
- Fill in the bar graph below based on the results you calculated from R. Remember: a population growth rate (λ) below 1 is declining and above 1 is increasing
- Provide brief answers to the following questions.
- What can you conclude about the results above regarding how effective biological control would be for Lespedeza cuneata?
- How do your results differ from the predictions you made on questions 4 and 5?
- What are some potential explanations for why your predictions differ from the actual results?
9. Calculate the elasticity matrix for the plants in the control treatment. To do this, you must first make sure the matrix in the 'lespedeza' program is showing the values for the control treatment (i.e., the small to medium transition should be set at 0.64), and re-run the program as in step 7a. In the console, you can type in 'A' to see your matrix, 'lambda' to see the population growth rate associated with that matrix, and 'e' to see the elasticity matrix. Once you have your elasticity matrix, proceed to the next step.
10. Provide brief answers to the following questions (also available as Handout 6) based on the elasticity analysis of the population growth rate of the invasive Lespedeza cuneata.
- Based on the results of the elasticity analysis, what vital rate (specific transition or reproduction of specific stage class) is population growth rate most sensitive to, or rather, what vital rate contributes most to λ?
- Recall: the small to medium transition was affected by herbivory. What is the elasticity of this transition? Is it high or low?
- How does your hypotheses from question 5c relate to results from the elasticity analysis? (Use your responses to questions 1 and 2 above to help answer this question.)
- Based on your elasticity analysis, which vital rates should managers focus on if they want to reduce the population growth rate of Lespedeza cuneata? Give some suggestions for how this might be accomplished.